machine learning tutorial summary

发表于 |

背景

auc的可行性计算

理论上，基于(fpr,tpr)对图形进行累积可以计算出auc，但是需要进行累加矩形面积，略显啰嗦。实际中可以采用更易计算的公式直接推导即可。一个常用的计算公式如下图所示

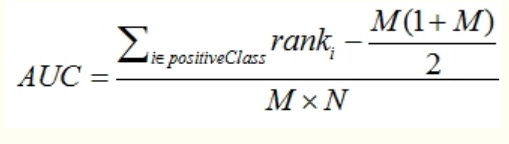
其中M是正样本，N是负样本个数。

​ 使用此公式的前提是instance计算pctr后按照pctr进行降序排列，然后观察所有的(正样本，负样本) 这种pair，正样本排在负样本前面。auc即使衡量在这种排序下，正样本排在负样本前面的比例有多少，按照概率的定义，当样本足够多的情况下，这种比例值即是概率的值。

当所有正样本都排在所有负样本的前面时候，那么此时排列是最理想的，此时auc应该是1.0

对于n个样本的ins，定义第一个样本的rank为n，那么第二个样本的rank就n-1，那么正样本排在负样本这种pair的个数就是$$\Sigma{正样本rank值} - (正样本，正样本)个数$$

对于M个正样本来说，第一个正样本与后面的每个正样本组合，形成M-1个;对于第二个正样本来说，与后面的每个正样本形成M-2个组合，依此类推…，总共形成的（正样本，正样本）的个数为$$(M-1)+(M-2)+…+(1)$$

如基于如下instance计算后的pctr数据

pctr y rank
0.95 1 5
0.90 0 4
0.81 1 3
0.75 0 2
0.6 0 1

其中M=2，N=3，n=M+N = 5,
正样本的rank之和计算为：

$$\sum{正样本rank}$$

$\sum{正样本rank}$

其中
$\frac{2(2+1)}{2} = 3$
计算出其$auc = \frac{8-3}{3*2}$
即$\frac{5}{6}$ = 0.8333。

如果不同score会依次给出一个rank值，如果score值相同，那么rank值也给予相同的值。

$$
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix} \tag{1}
$$

$$
\begin{equation}
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix}+
\begin{bmatrix}
10 & 11 & 12 \\
13 & 14 & 15 \\
16 & 17 & 18
\end{bmatrix}=
\begin{bmatrix}
11 & 13 & 15 \\
17 & 19 & 21 \\
23 & 25 & 27
\end{bmatrix}
\end{equation}
$$

附一段最近在使用的计算auc的scala代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
def calcAUC(f : scala.collection.Iterable[( String,Array[Double] )]) : Double = {
  var auc = 0.0 
  val tuples = new ArrayBuffer[(Double,Array[Double])];
  val tuples2 = new ArrayBuffer[(Double,Array[Double])];
  f.foreach(x => {
    val ctr:Double =  x._2(0)
    tuples += ((ctr,Array(x._2(1),x._2(2))))
  })
  tuples.groupBy(_._1).map(x => {
    var sum_1 = 0.0
    var sum_2 = 0.0
    x._2.foreach(f=>{
      sum_1 += f._2(0)
      sum_2 += f._2(1)
    })
    tuples2 += ((x._1,Array(sum_1,sum_2)))
    })
  var last_tp = 0.0
  var last_fp = 0.0
  tuples2.sortBy(f => f._1)(Ordering[Double].reverse).foreach( f => {
    val tp = f._2(0)
    val fp = f._2(1)
    val delta_x = fp 
    val delta_y = tp
    auc += (last_tp*2 + delta_y)*delta_x*0.5
    last_tp += delta_y
    last_fp += delta_x
  })
  auc = auc/(last_tp*last_fp)
  return auc
}

这里进行简答的说明

  1. input接受的是一个List，其中每个元素都是一个包含三个元素的tuple，组成形式为 tuple(ctr, click, noclick)

  2. 其中tuple的ctr是按照相同ctr进行过聚合，然后进行倒排，也就是代码中的reverse

  3. 在二维的XY轴中，以fp作为x轴，以tp作为y轴，delta_x表示当前的nonclick，delta_y表示当前的click数值，这样绘制图形，每个ctr都会绘制出一个包含三角形+一个矩形的形状

  4. 计算这个形状的面积 = 三角形面积 + 矩形面积：其中矩形面积是

    矩形 = dealt_x * last_tp

    三角形面积 = dealt_x delta_y 0.5

    合并两个面积和 = (2last_tp + delta_y) delta_x 0.5，而总面积是last_fp last_tp，前者除以后者就是roc线下的面积，也就是auc的数值。

–EOF –