背景
参与训练数据的分布为$L(x)$,而基于数据train出的model,记作$\vec{L(x)}$,基于此,在train data上进行计算预估值与实际目标的差的期望$E(\vec{L(x)}-L(x))$,这即为bais。
简单的说,bais也就是经验风险误差,衡量的是model在train data上的预估与真实情况的偏差。一般来说,bais小,那么对train data拟合的越好。
而Variance则是用来标识$\vec{L(x)}$自身的稳定性。采用相同的算法,不同的train data,预估出不同的$\vec{L_{1}{x}}$,$\vec{L_{2}{x}}$,…. $\vec{L_{n}{x}}$,针对同一个样本ins,计算对应的值$y_1$,$y_2$,$y_3$,…,$y_n$,那么$y$值的Variance就是model的Variance。
从common sense上来说,同样算法+同样ins,计算的$y$值应该近似,此时的方差就比较少。如果$y$值忽高忽低,那么Variance就比较高了。
目标上,我们期望能够拿到variance比较小的model,这里是用打靶场景来描述bais以及variance的关系
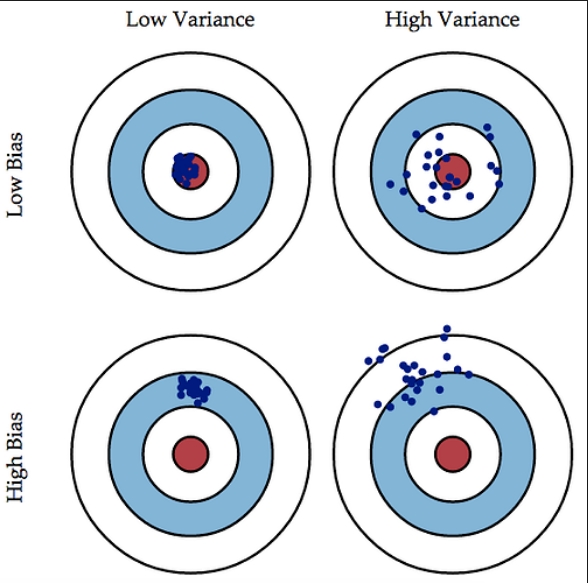
靶心相当于实际应该预测的结果。在train data上low bais,那么数据都是接近靶心的。如果是high bais,那么在train data上都偏离了,就没必要在validate dataset上继续实验了。
同样的,如果是low bais的前提下,再看variance,如果是low variance的,那么预测的值分布是集中的;而high Variance下预测的值是比较分散的。
因此,可以说,理想的model应该是low bais+ low variance的model。
模型复杂度
一般的,model的误差是bais以及Variance之和。如下图阐述了model逐渐增加复杂度的渐变过程。
- 最初model简单,参数少,对train data也是high bais,当然如果拿来预估,基本也是high variance的。
- 然后增加参数,即增加了模型复杂度,对train data的拟合也会越来越好,bais逐渐减少。同时high Variance也会逐渐减少。
- 继续增加模型复杂度,比如增加更多特征,对train data的拟合更加完美,那么对实际数据的泛化能力也会逐渐减少,此时Variance会逐渐升高,即变的high Variance了。
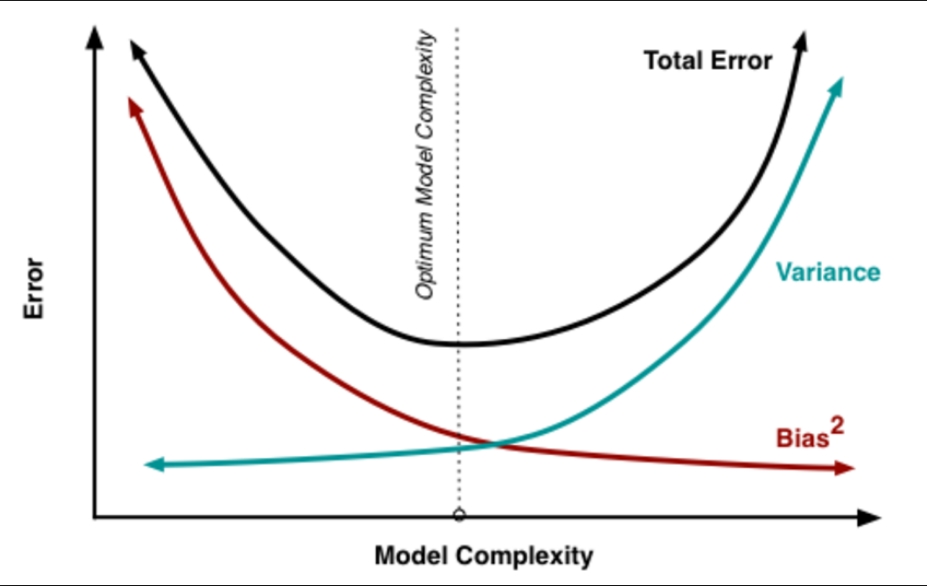
因此,当bais以及Variance都变的最小时候,model 的complexity为最佳。
Handle underfitting and overfitting
NG的课程中给出了如何处理underfitting以及overfitting的方法:
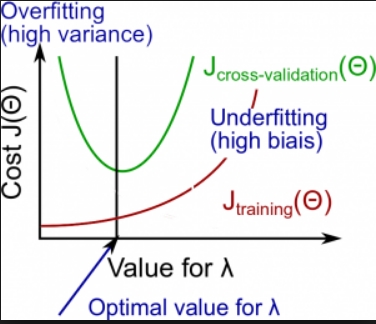
- 首先判断在traindata上是不是high bias,如果是,那么说明拟合不够。
- 从common sense上来说,欠拟合有可能是迭代次数不够,没拿到最佳的w;那么可以尝试增加iteration来看看最终的w是否ok。
- 是不是特征数太少,拟合不够,可以增加更多特征。或者训练个更复杂的model。
- 正则化会使得模型稀疏,可能会导致欠拟合。减少正则化是个不错选择。
- 考虑其他model算法。
- 如果在traindata上bais上比较低,那么说明对traindata的拟合ok,那么就要看下对真实数据的predict是否ok,即看validate dataset上的Variance。如果是high Variance。那么尝试从一下几个方向来减少Variance。
1、从common sense上来说,traindata上有比较好的表现,但是在validate data上却表现差,说明存在过拟合了,直接的结论就是模型的复杂度是不是过高了,因此可以减少模型复杂度方向上来考虑,比如增加正则化。
2、train data太少,导致了过拟合,尝试获取更多traindata
3、特征使用太多,尝试减少部分特征。
4、尝试简单model算法。
总结
总的来说,bais和Variance两个指标,其实是两个比较典型的指标,用来指导我们进行算法调优,基本的步骤就是从bais入手,确定拿到low bais的情况下再从validate dataset上调优Variance。
2017.06.14
参考
[1] https://liam0205.me/2017/03/25/bias-variance-tradeoff
–EOF–